how to find the p value given z

When yous test a hypothesis about a population, you can apply your test statistic to make up one's mind whether to reject the null hypothesis, H₀. You make this decision by coming upward with a number, called a p-value.

A p-value is a probability associated with your critical value. The critical value depends on the probability you are allowing for a Blazon I error. It measures the chance of getting results at least as potent as yours if the claim (H₀) were truthful.

The following figure shows the locations of a exam statistic and their respective conclusions.

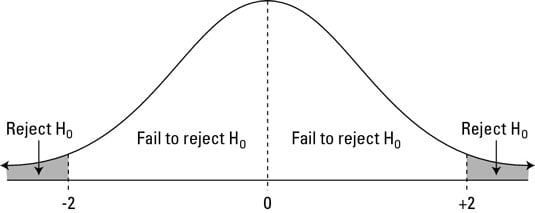
Decisions for H_a: non-equal-to.

Note that if the alternative hypothesis is the less-than culling, you decline H₀ merely if the test statistic falls in the left tail of the distribution (below –2). Similarly, if H_a is the greater-than culling, you reject H₀ only if the examination statistic falls in the correct tail (higher up 2).

To find the p-value for your test statistic:

Look up your test statistic on the appropriate distribution — in this case, on the standard normal (Z-) distribution (run into the following Z-tables).
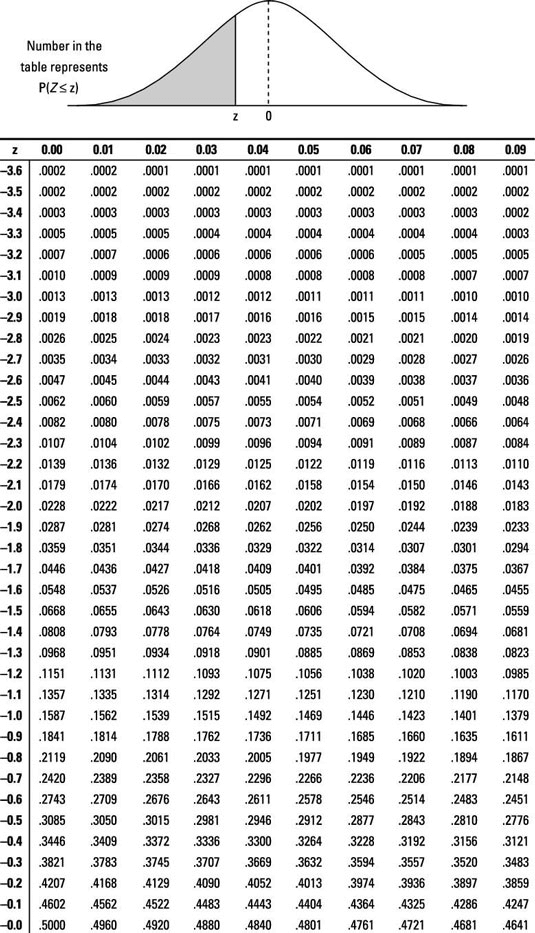
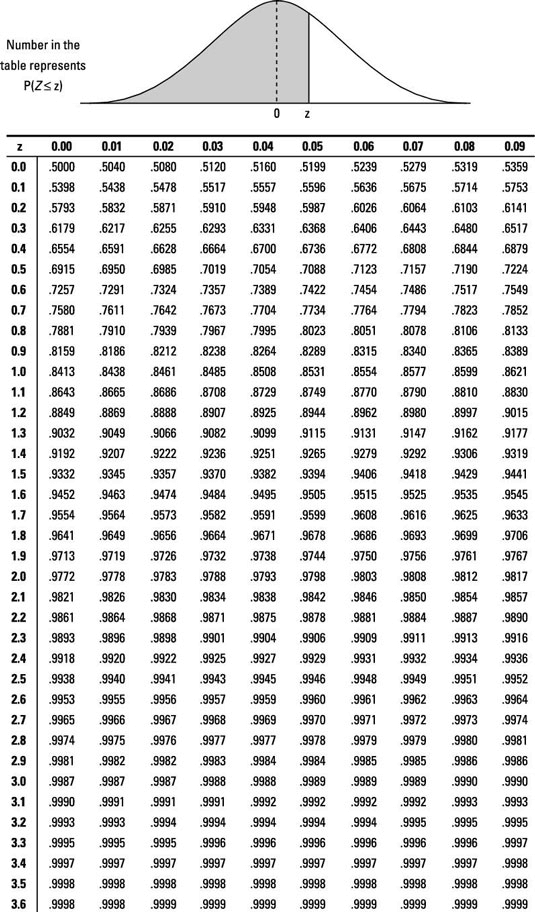
Discover the probability that Z is beyond (more than extreme than) your test statistic:
1. If H_a contains a less-than alternative, find the probability that Z is less than your test statistic (that is, look upward your test statistic on the Z-tabular array and find its respective probability). This is the p-value. (Note: In this case, your exam statistic is commonly negative.)
2. If H_a contains a greater-than alternative, find the probability that Z is greater than your test statistic (await up your test statistic on the Z-table, find its respective probability, and subtract it from one). The upshot is your p-value. (Notation: In this instance, your test statistic is commonly positive.)
3. If H_a contains a non-equal-to alternative, detect the probability that Z is across your test statistic and double it. There are two cases:
  
  If your test statistic is negative, beginning find the probability that Z is less than your test statistic (look up your examination statistic on the Z-table and notice its corresponding probability). Then double this probability to get the p-value.
  
  If your exam statistic is positive, start find the probability that Z is greater than your test statistic (await up your test statistic on the Z-table, find its corresponding probability, and subtract it from one). Then double this result to get the p-value.

Suppose you are testing a merits that the percentage of all women with varicose veins is 25%, and your sample of 100 women had 20% with varicose veins. And then the sample proportion p=0.20. The standard mistake for your sample per centum is the foursquare root of p(i-p)/n which equals 0.04 or 4%. You find the test statistic by taking the proportion in the sample with varicose veins, 0.xx, subtracting the claimed proportion of all women with varicose veins, 0.25, and then dividing the upshot past the standard fault, 0.04. These calculations give you a test statistic (standard score) of –0.05 divided by 0.04 = –ane.25. This tells yous that your sample results and the population claim in H₀ are 1.25 standard errors apart; in particular, your sample results are one.25 standard errors below the claim.

When testing H₀: p = 0.25 versus H_a: p < 0.25, you find that the p-value of -1.25 by finding the probability that Z is less than -1.25. When you look this number up on the above Z-table, you lot find a probability of 0.1056 of Z being less than this value.

Note: If you had been testing the two-sided culling,

the p-value would be two ∗ 0.1056, or 0.2112.

If the results are likely to have occurred under the claim, then you fail to reject H₀ (like a jury decides not guilty). If the results are unlikely to have occurred under the claim, and then you decline H₀ (similar a jury decides guilty).